※ 본 포스팅은 밑바닥부터 시작하는 딥러닝에 기재된 내용과 사진을 기반으로 포스팅하였습니다.

깃허브(예제 소스) : GitHub - kchcoo/WegraLee-deep-learning-from-scratch
GitHub - kchcoo/WegraLee-deep-learning-from-scratch
Contribute to kchcoo/WegraLee-deep-learning-from-scratch development by creating an account on GitHub.
github.com
밑바닥부터 시작하는 딥러닝 7장은 합성곱 신경망(Convolutional Neural Network, CNN)을 학습하게 된다.
CNN은 이미지 인식과 음성 인식 등 다양한 곳에 사용된다. 특히 이미지 인식 분야에서 딥러닝을 활용한 기법은 CNN이 기초라고 할 수 있다.

7.1 전체 구조
CNN은 합성곱 계층과 풀링 계층이 새롭게 등장한다. 지금까지 본 신경망은 인접하는 계층의 모든 뉴런과 결합되어 있다. 이를 완전연결(Fully-connected, 전연결)이라고 한다.


CNN은 'Conv-ReLU-(pooling)'으로 바뀌었다고 생각할 수 있고, 출력에 가까운 층에서는 'Affine-ReLU' 구성을 사용하고 있습니다. 그리고 마지막 출력 계층은 'Affine-softmax' 조합을 그대로 사용한다.
7.2 합성공 계층
CNN에는 패딩, 스트라이드 등의 고유의 용어가 등장한다. 완전연결과 CNN의 다른 점은 각 계층 사이에는 3차원 데이터같이 입체적인 데이터가 흐른다는 점이다. 합성곱 계층의 입출력 데이터를 특징 맵, 입력 데이터를 입력 특징 맵, 출력 데이터를 출력 특징 맵이라고 한다.
7.2.1 완전연결 계층의 문제점
완전 연결 계층의 문제점은 데이터의 현상이 무시된다는 점이다. 예를 들어 입력 데이터가 이미지인 경우 이미지는 통상 세로·가로·채널(색상)로 구성된 3차원 형상이며, 이 형상에는 소중한 공간적 정보가 담겨 있다. 그러나 완전 연결 계층에 입력할 때는 3차원 데이터를 평평한 1차원 데이터로 평탄화해줘야 한다. 이렇게 되면 현상을 무시하고 모든 입력 데이터를 동등한 뉴런으로 취급하여 현상에 담긴 정보를 살릴 수 없다는 문제가 생긴다. 하지만 CNN에서는 이미지처럼 형상을 가진 데이터를 제대로 이해할 가능성이 있다.

7.2.2 합성곱 연산
합성곱 연산은 이미지 처리에서 말하는 필터 연산에 해당한다. 문헌에 따라 필터를 커널이라고 칭한다.

합성곱 연산은 필터의 윈도우를 일정 간격으로 이동해가며 입력 데이터를 적용한다. 입력과 필터에서 대응하는 원소끼
리 곱한 후 그 총합을 구한다. 이 계산을 단일 곱셈-누산(fused multiply-add, FMA)라고 한다.
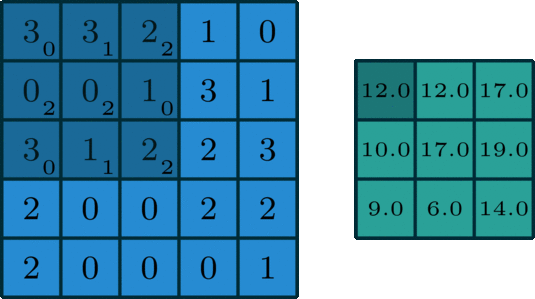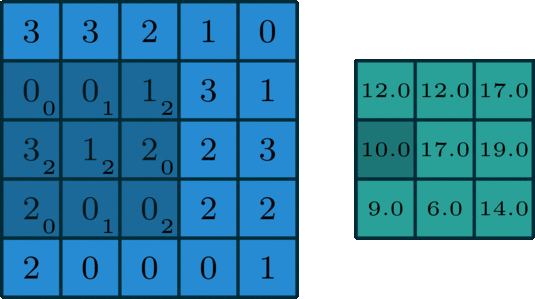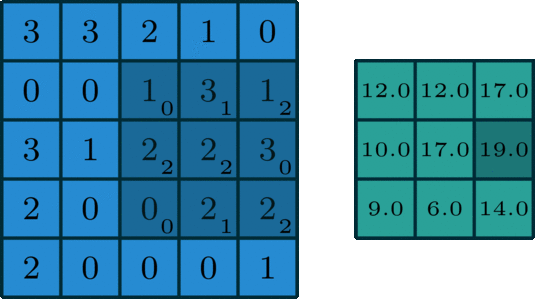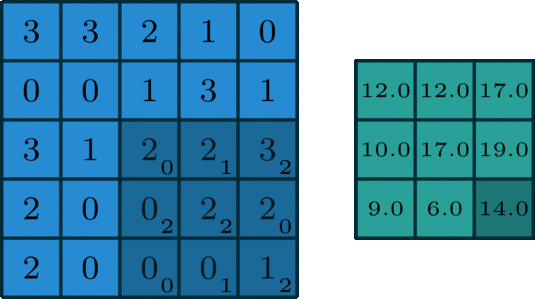
CNN에서는 필터의 매개변수가 '가중치'에 해당하고, 편향은 필터를 적용한 후의 데이터에 더해진다. 편향은 항상 하나(1x1)만 존재한다.
7.2.3 패딩
패딩은 합성곱 연산을 수행하기 전에 입력 데이터 주변을 특정 값(0으로 채우는 것을 제로 패딩이라고 한다.)으로 채우는 것을 말한다.

패딩은 출력 크기를 조정할 목적으로 사용한다. 합성곱 연산을 거칠 때마다 크기가 작아지면 어느 시점에서는 출력의 크기가 1이 되어버린다. 이 뜻은 합성곱 연산을 적용할 수 없다는 뜻이다. 이러한 이유로 패딩을 사용한다.
7.2.4 스트라이드
스트라이드는 필터를 적용하는 위치의 간격, 보폭을 뜻한다. 스트라이드는 필터를 적용하는 간격을 지정한다.

패딩(P), 스트라이드(S), 입력 크기((H,W)), 필터 크기((FH, FW))를 가지고 출력 크기((OH, OW))를 계산할 수 있다. 단, 정수로 나눠 떨어지는 값이어야 한다.

7.2.5 3차원 데이터의 합성곱 연산
3차원 데이터로 합성곱 연산을 할 때는 채널을 생각해야한다. 단, 주의해야 할 점은 입력 데이터의 채널 수와 필터의 채널 수가 일치해야 한다.

7.2.6 블록으로 생각하기, 7.2.7 배치 처리
3차원 합성곱 연산은 데이터와 필터를 직육면체 블록으로 생각하면 쉽다.

합성곱 연산에서의 배치 처리는 데이터를 (데이터 수, 채널 수, 높이, 연산 - F, FN, OH, OW) 순으로 저장한다. 신경망에 4차원 데이터가 하나 흐를 때마다 데이터 N개에 대한 합성곱 연산이 이뤄진다.
7.3 풀링 계층
풀링은 세로·가로 방향의 공간을 줄이는 연산이다. 풀링에는 평균 풀링(대상 영역의 평균을 계산)과 최대 풀링이 있는데 이 책에서는 최대 풀링만을 다룬다. 최대 풀링은 최댓값을 구하는 연산으로 2x2 최대 풀링이면 2x2 대상 영역의 크기를 뜻한다.

7.3.1 풀링 계층의 특징
1. 학습해야 할 매개변수가 없다.
최댓값이나 평균을 취하는 명확한 처리이므로 특별히 학습할 것이 없다.
2. 채널 수가 변하지 않는다.
채널마다 독립적으로 계산하기 때문에 입력 데이터의 채널 수 그대로 출력 데이터로 내보냅니다.

3. 입력의 변화에 영향을 적게 받는다. (강건하다)
입력 데이터가 조금 변해도 풀링의 결과는 잘 변하지 않습니다.

7.4 합성곱/풀링 계층 구현하기
7.4.2 im2col로 데이터 전개하기
합성곱 연산을 구현하려면 for문을 겹겹이 써야 한다. 그렇게 되면 넘파이에 for 문을 사용하면 성능이 떨어진다는 단점이 있다. 그래서 for문 대신 im2col이라는 함수를 사용했다.
im2col('image to column' - '이미지에서 행렬로')은 입력 데이터를 필터링(가중치 계산) 하기 좋게 전개하는(펼치는) 함수이다. 4차원 데이터를 2차원으로 변환하는 함수이다.

im2col의 단점은 메모리를 많이 소비한다는 것이다. 필터의 적용 영역이 겹치게 되면 im2col로 전개한 후의 원소수가 원래 블록의 원소 수보다 많아지기 때문이다. 하지만 컴퓨터는 큰 행렬을 묶어서 계산하는 데 탁월하다.

im2col을 이용해서 2차원으로 출력한 데이터는 CNN에서는 4차원 배열로 저장하므로 reshape을 사용해서 다시 4차원으로 변형한다.
7.4.4 풀링 계층 구현하기
풀링 계층 구현 같은 경우 합성곱 계층과 유사하지만 채널 쪽이 독립적이라는 점이 합성곱 계층과 다른 점이다.

풀링 계층 구현은 다음 세 단계로 진행된다.
1. 입력 데이터를 전개한다.
2, 행별 최댓값을 구한다.
3. 적절한 모양으로 성형한다.
7.6 CNN 시각화하기
합성곱 계층 (1층째) 필터를 이미지로 나타낸 것이다.

학습 전 필터는 무작위로 초기화되고 있어 흑백의 정도에 규칙성이 없다. 하지만 학습을 마친 필터는 규칙성이 있는 이미지이다. 흰색에서 검은색으로 점차 변화하는 필터와 덩어리가 진 필터 등, 규칙을 띄는 필터로 바뀌었다.
7.6.2 층의 깊이에 따른 추출 정보 변화
1번째 층의 합성곱 계층에서는 에지나 블록 등의 저수준 정보가 추출된다. 계층이 깊어질수록 추출되는 정보(강하에 반응하는 뉴런)는 더 추상화된다는 것을 알 수 있다.
7.7 대표적인 CNN
CNN 네트워크 가운데 중요한 CNN의 원조인 LeNet과 딥러닝이 주목받도록 이끈 AlexNet을 소개한다.
7.7.1 LeNet
LeNet은 손글씨 숫자를 인식하는 네트워크이다. LeNet는 합성곱 계층과 서브 샘플링 계층(단순히 원소를 줄이기)을 반복하고, 마지막으로 완전 연결 계층을 거치면서 결과를 출력한다.

LeNet과 CNN에는 몇가지 차이점이 있다.
1. 활성화 함수이다.
LeNet은 시그모이드 함수를 사용하고 CNN은 ReLU함수를 사용한다.
2. 풀링 계층이다.
LeNet은 서브샘플링을 하여 중간 데이터의 크기를 줄이지만 CNN은 최대 풀링을 이용한다.
7.2.2 AlexNet
AlexNet은 LeNet에서의 큰 구조와 다르지 않다.

- 활성화 함수로 ReLU를 이용한다.
- LRN이라는 국소적 정규화를 실시하는 계층을 이용한다.
- 드롭아웃을 사용한다.
7.8 정리
- CNN은 지금까지의 완전연결 계층 네트워크에 합성곱 계층과 풀링 계층을 새로 추가한다.
- 합송곱 계층과 풀링 계층은 im2col을 이용하면 간단하고 효율적으로 구현할 수 있다.
- CNN을 시각화해보면 계층이 깊어질수록 고급 정보가 추출되는 모습을 확인할 수 있다.
- 대표적인 CNN에는 LeNet과 AlexNet이 있다.
- 딥러닝의 발전에는 빅데이이터와 GPU가 크게 기여했다.
'ML 관련 스터디' 카테고리의 다른 글
| 펭귄브로의 3분 딥러닝 파이토치맛 3장 스터디 (0) | 2023.12.13 |
|---|---|
| 펭귄브로의 3분 딥러닝 파이토치맛 4장 스터디 (0) | 2023.12.13 |
| 펭귄브로의 3분 딥러닝 파이토치맛 5장 스터디 (0) | 2023.12.13 |
| 펭귄브로의 3분 딥러닝 파이토치맛 6장 스터디 (0) | 2023.12.13 |
| 펭귄브로의 3분 딥러닝 파이토치맛 7장 스터디 (0) | 2023.12.13 |



